In this paper, a novel twenty-three-point second-order rotatable design is formulated utilizing trigonometric functions. Design of experiments plays a crucial role in various industries and research fields to investigate the relationship between multiple variables and their effects on a response variable. In particular, second order rotatable designs are widely used due to their ability to efficiently estimate the main, interaction, and curvature effects. Nevertheless, creating designs with a substantial number of points poses difficulties. This study concentrates on developing a second-order rotatable design with twenty-three points utilizing trigonometric functions. Trigonometric functions offer a systematic approach to distribute the points uniformly in the design space, thereby ensuring the optimal coverage of the experimental region. The proposed construction utilizes the properties of sine and cosine functions to generate a balanced and efficient design. The methodology involves dividing the design space into equidistant sectors and assigning the points using the trigonometric functions. By carefully selecting the starting angle and the angular increment, a complete and orthogonal design is achieved. The design is rotatable, meaning it can be rotated to any desired orientation without impairing the statistical properties of the design. Through this construction, the design effectively captures the main effects, interaction effects, and curvature effects. This enables reliable estimation of the model parameters, leading to accurate predictions and efficient optimization. Additionally, the design is efficient in terms of minimizing the number of experimental runs required, thereby reducing costs and time. The suggested second-order rotatable design comprising twenty-three points and employing trigonometric functions exhibits its superiority when compared to conventional designs. It offers a systematic and straightforward approach to construct a balanced and efficient design for studying the relationships between multiple variables. The design's rotatability ensures flexibility in experimental settings, making it a valuable tool for researchers and practitioners in various fields.
| Published in | American Journal of Theoretical and Applied Statistics (Volume 13, Issue 3) |
| DOI | 10.11648/j.ajtas.20241303.11 |
| Page(s) | 46-56 |
| Creative Commons |
This is an Open Access article, distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution and reproduction in any medium or format, provided the original work is properly cited. |
| Copyright |
Copyright © The Author(s), 2024. Published by Science Publishing Group |
Curvature Effects, Sine and Cosine Functions, Augmented
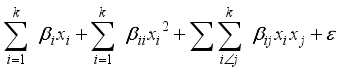 (1)
(1) 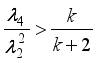 =
= Set composition of class | z1 = 3s | Z2=G(,) | Z3=G(,) | z1 ++ z3 |
|---|---|---|---|---|
Number of points | For s=5 = 15 points | 4 points | 4 points | 23 points |
𝑁 ∑ 𝑥2 𝑖𝑢 𝑢=1 |
|
|
|
|
𝑁 ∑ 𝑥4 𝑖𝑢 𝑢=1 |
|
|
|
|
𝑁 ∑ 𝑥2 𝑥2 𝑖𝑢 j𝑢 𝑢=1 |
|
|
|
|
𝑁 𝑁 ∑ 𝑥4 − 3 ∑ 𝑥2 𝑥2 𝑖𝑢 𝑖𝑢 j𝑢 𝑢=1 𝑢=1 |
|
|
|
|
Coded levels | Natural levels | Weight_yield | ||||
|---|---|---|---|---|---|---|
-1.384437 | 0 | 1.384437 | 34.5653 | 25 | 45.3277 | 52 |
1.384437 | 0 | 1.384437 | 35.4347 | 25 | 45.3277 | 87 |
-1.384437 | 0 | -1.384437 | 34.5653 | 25 | 44.6723 | 73 |
1.384437 | 0 | -1.384437 | 35.4347 | 25 | 44.6723 | 55 |
-1.384437 | 1.384437 | 0 | 34.5653 | 25.2014 | 45 | 74 |
1.384437 | 1.384437 | 0 | 35.4347 | 25.2014 | 45 | 58 |
-1.384437 | -1.384437 | 0 | 34.5653 | 24.7986 | 45 | 92 |
1.384437 | -1.384437 | 0 | 35.4347 | 24.7986 | 45 | 75 |
0 | 1.384437 | -1.384437 | 35 | 25.2014 | 45.3277 | 72 |
0 | 1.384437 | 1.384437 | 35 | 25.2014 | 44.6723 | 78 |
0 | -1.384437 | 1.384437 | 35 | 24.7986 | 45.3277 | 89 |
0 | -1.384437 | -1.384437 | 35 | 24.7986 | 44.6723 | 72 |
-1.384437 | 0 | 0 | 34.5653 | 25 | 45 | 65 |
1.384437 | 0 | 0 | 35.4347 | 25 | 45 | 56 |
0 | -1.384437 | 0 | 35 | 24.7986 | 45 | 56 |
0 | -1.384437 | 0 | 35 | 25.2014 | 45 | 77 |
0 | 0 | 1.384437 | 35 | 25 | 45.3277 | 56 |
0 | 0 | -1.384437 | 35 | 25 | 44.6723 | 59 |
-1.384437 | 0 | 0 | 34.5653 | 25 | 45 | 62 |
1.384437 | 0 | 0 | 35.4347 | 25 | 45 | 60 |
0 | 1.384437 | 0 | 35 | 25.2014 | 45 | 60 |
0 | -1.384437 | 1.384437 | 35 | 24.7986 | 45.3277 | 80 |
0 | 0 | -1.384437 | 35 | 25 | 44.6723 | 68 |
X= | [,1] | [,2] | [,3] | [,4] | [,5] | [,6] | [,7] | [,8] | [,9] | [,10] |
|---|---|---|---|---|---|---|---|---|---|---|
[1,] | 1 | -1.384437 | 0.000000 | 1.384437 | 1.916667 | 0.000000 | 1.916667 | 0.000000 | -1.916667 | 0.000000 |
[2,] | 1 | 1.384437 | 0.000000 | 1.384437 | 1.916667 | 0.000000 | 1.916667 | 0.000000 | 1.916667 | 0.000000 |
[3,] | 1 | -1.384437 | 0.000000 | -1.384437 | 1.916667 | 0.000000 | 1.916667 | 0.000000 | 1.916667 | 0.000000 |
[4,] | 1 | 1.384437 | 0.000000 | -1.384437 | 1.916667 | 0.000000 | 1.916667 | 0.000000 | 1.916667 | 0.000000 |
[5,] | 1 | -1.384437 | 1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | -1.916667 | 0.000000 | 0.000000 |
[6,] | 1 | 1.384437 | 1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 1.916667 | 0.000000 | 0.000000 |
[7,] | 1 | -1.384437 | -1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 1.916667 | 0.000000 | 0.000000 |
[8,] | 1 | 1.384437 | -1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | -1.916667 | 0.000000 | 0.000000 |
[9,] | 1 | 0.000000 | 1.384437 | 1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 0.000000 | 1.916667 |
[10,] | 1 | 0.000000 | 1.384437 | -1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 0.000000 | -1.916667 |
[11,] | 1 | 0.000000 | -1.384437 | 1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 0.000000 | -1.916667 |
[12,] | 1 | 0.000000 | -1.384437 | -1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 0.000000 | 1.916667 |
[13,] | 1 | -1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[14,] | 1 | 1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[15,] | 1 | 0.000000 | -1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[16,] | 1 | 0.000000 | 1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[17,] | 1 | 0.000000 | 0.000000 | 1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 |
[18,] | 1 | 0.000000 | 0.000000 | -1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 |
[19,] | 1 | -1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[20,] | 1 | 1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[21,] | 1 | 0.000000 | 1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
[22,] | 1 | 0.000000 | -1.384437 | 1.384437 | 0.000000 | 1.916667 | 1.916667 | 0.000000 | 0.000000 | -1.916667 |
[23,] | 1 | 0.000000 | 0.000000 | -1.384437 | 0.000000 | 0.000000 | 1.916667 | 0.000000 | 0.000000 | 0.000000 |
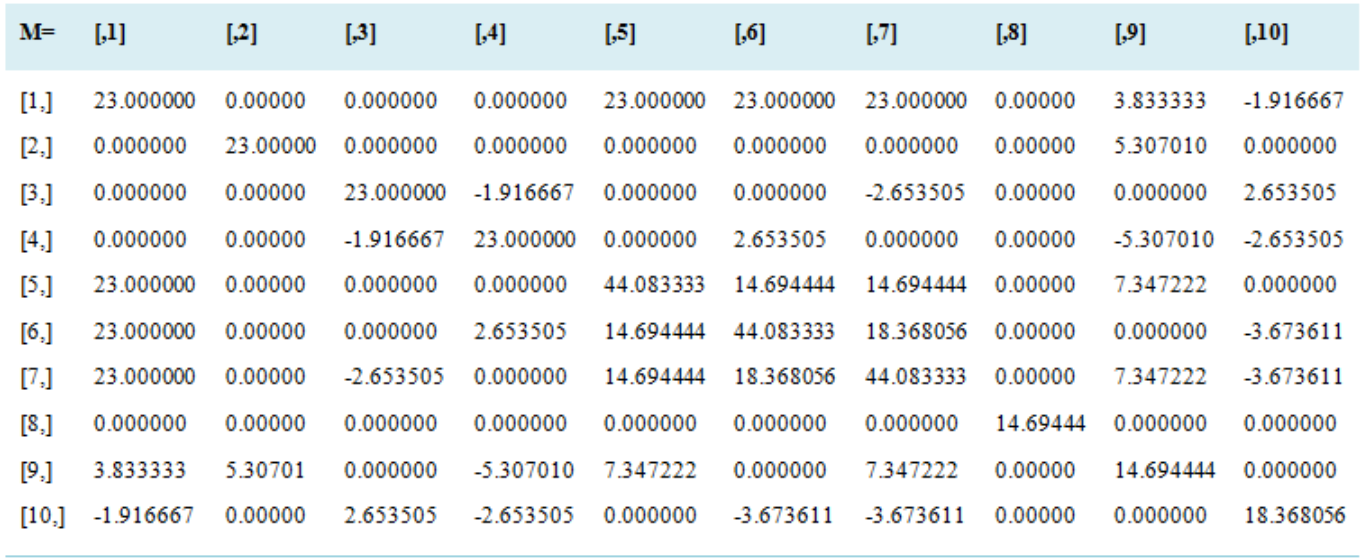
N= | [,1] | [,2] | [,3] | [,4] | [,5] | [,6] | [,7] | [,8] | [,9] | [,10] |
|---|---|---|---|---|---|---|---|---|---|---|
[1,] | 0.51440 | -0.010416 | -0.015942 | 0.02581 | -0.17459 | -0.146033 | -0.15791 | 0.00000 | 0.04514 | -0.001080 |
[2,] | -0.01041 | 0.048992 | 0.000377 | -0.00560 | 0.006946 | 0.000562 | 0.00685 | 0.0000 | -0.02389 | -0.000467 |
[3,] | -0.01594 | 0.000377 | 0.045268 | 0.00242 | 0.00501 | 0.002667 | 0.008056 | 0.0000 | -0.0016 | -0.005707 |
[4,] | 0.025811 | -0.00560 | 0.002428 | 0.05093 | -0.01159 | -0.00815 | -0.00958 | 0.0000 | 0.024277 | 0.006150 |
[5,] | -0.17459 | 0.00694 | 0.00501 | -0.01159 | 0.08848 | 0.04149 | 0.04942 | 0.0000 | -0.03010 | -0.00243422 |
[6,] | -0.14603 | 0.00056 | 0.00266 | -0.00815 | 0.04149 | 0.072026 | 0.03326 | 0.0000 | -0.00243 | 0.004256 |
[7,] | -0.15791 | 0.00685 | 0.00805 | -0.0095 | 0.04942 | 0.03326 | 0.0804 | 0.0000 | -0.02969 | 0.003723 |
[8,] | 0.00000 | 0.00000 | 0.000000 | 0.0000 | 0.0000 | 0.00000 | 0.00000 | 0.06805 | 0.00000 | 0.00000 |
[9,] | 0.045145 | -0.02389 | -0.001636 | 0.0242 | -0.03010 | -0.00243 | -0.02969 | 0.0000 | 0.10357 | 0.002027 |
[10,] | -0.00108 | -0.00046 | -0.00570 | 0.00615 | -0.00243 | 0.00425 | 0.0037 | 0.0000 | 0.00202 | 0.0576387 |
Term | Coef | SE Coef | T-Value | P-Value | VIF |
|---|---|---|---|---|---|
Constant | 52.27 | 6.23 | 8.40 | 0.000 | |
Poultry | -2.25 | 2.55 | -0.88 | 0.395 | 1.00 |
Rabbit | -2.57 | 2.61 | -0.99 | 0.341 | 1.04 |
Goat | 0.73 | 2.61 | 0.28 | 0.783 | 1.04 |
Poultry *Poultry | 7.34 | 4.79 | 1.53 | 0.149 | 1.68 |
Rabbit *Rabbit | 14.83 | 4.55 | 3.26 | 0.006 | 1.52 |
Goat*Goat | 8.57 | 4.55 | 1.88 | 0.082 | 1.52 |
Poultry *Rabbit | 0.25 | 4.43 | 0.06 | 0.956 | 1.00 |
Poultry *Goat | 13.25 | 4.43 | 2.99 | 0.010 | 1.00 |
Rabbit *Goat | -4.80 | 4.07 | -1.18 | 0.259 | 1.05 |
Source | DF | Adj SS | Adj MS | F-Value | P-Value |
|---|---|---|---|---|---|
Model | 9 | 2031.41 | 225.712 | 2.88 | 0.041 |
Linear | 3 | 146.42 | 48.806 | 0.62 | 0.613 |
Poultry | 1 | 60.75 | 60.750 | 0.78 | 0.395 |
Rabbit | 1 | 76.44 | 76.445 | 0.98 | 0.341 |
Goat | 1 | 6.19 | 6.189 | 0.08 | 0.783 |
Square | 3 | 866.40 | 288.799 | 3.69 | 0.040 |
Poultry *Poultry | 1 | 184.09 | 184.094 | 2.35 | 0.149 |
Rabbit *Rabbit | 1 | 831.89 | 831.888 | 10.62 | 0.006 |
Goat *Goat | 1 | 277.61 | 277.613 | 3.54 | 0.082 |
2-Way Interaction | 3 | 811.58 | 270.526 | 3.45 | 0.048 |
Poultry *Rabbit | 1 | 0.25 | 0.250 | 0.00 | 0.956 |
Poultry*Goat | 1 | 702.25 | 702.250 | 8.96 | 0.010 |
Rabbit *Goat | 1 | 109.08 | 109.078 | 1.39 | 0.259 |
Error | 13 | 1018.33 | 78.333 | ||
Lack-of-Fit | 8 | 780.33 | 97.541 | 2.05 | 0.223 |
Pure Error | 5 | 238.00 | 47.600 | ||
Total | 22 | 3049.74 |
Model Summary | ||
|---|---|---|
S | R.sq | R.sq (adj) |
8.85061 | 86.61% | 73.49% |
ASORD | Augmented Second Order Rotatable Design |
| [1] | Ahmed, F., Khan, S., & Jan, K. (2017). Optimization of nitrogen and phosphorus levels for wheat crop using response surface methodology. Pakistan Journal of Agricultural Sciences, 54(3), 591-595. |
| [2] | Atkinson, A. C. and Donev, A. N. (1992). Optimum experimental designs with SAS. Oford university press, UK. 34. |
| [3] | Bose, R. C., & Draper, N. R., (1959). Second order rotatable designs in three dimensions. The annals of mathematical statistics, 30(4), 1097-1112. |
| [4] | Box G. E., &Draper, N. R. (1975). Robust designs. Biometrika, 62(2), 347-352. |
| [5] | Box, G. E., & Draper, N. R. (1963). The choice of a second order rotatable design. Biometrika, 335-352. |
| [6] | Box, G. E., & Draper, N. R. (1965). The Bayesian estimation of common parameters from several responses. Biometrika, 52(3-4), 355-365. |
| [7] | Box, G. E. P., & Draper, N. R. (1980). The variance functions of the difference between two estimated responses. Journal of the royal statistical society. Series B. (Methodological). 79-82. |
| [8] | Box, G. E., & Hunter, J. S. (1957). Multifactor experimental designs for exploring response surfaces. The annals of mathematical statistics, 195-241. |
| [9] | Daniel Mwangi, I., Miano, M., & Macharia, L. (2019). Optimization of yields and yield components of sweet potatoes (Ipomea batatas (L.) Lam) using organic manure and phosphate fertilizer. Asian Journal of Probability and Statistics, 5(4), 1-13. |
| [10] | Demir, Ö., & Heck, A. (2013). A new learning trajectory for trigonometric functions. In Proceedings of the 11th international conference on technology in mathematics teaching (pp. 119-124). |
| [11] | Fang, K., Liu, M. Q., Qin, H., & Zhou, Y. D. (2018). Theory and application of uniform experimental designs (Vol. 221). Singapore: Springer. |
| [12] | Hemavathi, M., Varghese, E., Shekhar, S., & Jaggi, S. (2022). Sequential asymmetric third order rotatable designs (SATORDs). Journal of Applied Statistics, 49(6), 1364-1381. |
| [13] | Johnson, F. R., Lancsar, E., Marshall, D., Kilambi, V., Mühlbacher, A., Regier, D. A.,... & Bridges, J. F. (2013). Constructing experimental designs for discrete-choice experiments: report of the ISPOR conjoint analysis experimental design good research practices task force. Value in health, 16(1), 3-13. |
| [14] | Kosgei, M. K., Koske, J. K., & Mutiso, J. M. (2013). Construction of five-level modified third order rotatable design using a pair of balanced incomplete block designs. Journal of computational intelligence and systems sciences, 1, 10-18. |
| [15] | Street, D. J., & Burgess, L. (2004). Optimal and near-optimal pairs for the estimation of effects in 2-level choice experiments. Journal of Statistical Planning and Inference, 118(1-2), 185-199. |
APA Style
Matundura, D. M., Kosgei, M., Too, R. (2024). Construction of Twenty-Three Points Second Order Rotatable Design in Three Dimensions Using Trigonometric Functions. American Journal of Theoretical and Applied Statistics, 13(3), 46-56. https://doi.org/10.11648/j.ajtas.20241303.11
ACS Style
Matundura, D. M.; Kosgei, M.; Too, R. Construction of Twenty-Three Points Second Order Rotatable Design in Three Dimensions Using Trigonometric Functions. Am. J. Theor. Appl. Stat. 2024, 13(3), 46-56. doi: 10.11648/j.ajtas.20241303.11
AMA Style
Matundura DM, Kosgei M, Too R. Construction of Twenty-Three Points Second Order Rotatable Design in Three Dimensions Using Trigonometric Functions. Am J Theor Appl Stat. 2024;13(3):46-56. doi: 10.11648/j.ajtas.20241303.11
@article{10.11648/j.ajtas.20241303.11,
author = {Dennis Mwan Matundura and Mathew Kosgei and Robert Too},
title = {Construction of Twenty-Three Points Second Order Rotatable Design in Three Dimensions Using Trigonometric Functions
},
journal = {American Journal of Theoretical and Applied Statistics},
volume = {13},
number = {3},
pages = {46-56},
doi = {10.11648/j.ajtas.20241303.11},
url = {https://doi.org/10.11648/j.ajtas.20241303.11},
eprint = {https://article.sciencepublishinggroup.com/pdf/10.11648.j.ajtas.20241303.11},
abstract = {In this paper, a novel twenty-three-point second-order rotatable design is formulated utilizing trigonometric functions. Design of experiments plays a crucial role in various industries and research fields to investigate the relationship between multiple variables and their effects on a response variable. In particular, second order rotatable designs are widely used due to their ability to efficiently estimate the main, interaction, and curvature effects. Nevertheless, creating designs with a substantial number of points poses difficulties. This study concentrates on developing a second-order rotatable design with twenty-three points utilizing trigonometric functions. Trigonometric functions offer a systematic approach to distribute the points uniformly in the design space, thereby ensuring the optimal coverage of the experimental region. The proposed construction utilizes the properties of sine and cosine functions to generate a balanced and efficient design. The methodology involves dividing the design space into equidistant sectors and assigning the points using the trigonometric functions. By carefully selecting the starting angle and the angular increment, a complete and orthogonal design is achieved. The design is rotatable, meaning it can be rotated to any desired orientation without impairing the statistical properties of the design. Through this construction, the design effectively captures the main effects, interaction effects, and curvature effects. This enables reliable estimation of the model parameters, leading to accurate predictions and efficient optimization. Additionally, the design is efficient in terms of minimizing the number of experimental runs required, thereby reducing costs and time. The suggested second-order rotatable design comprising twenty-three points and employing trigonometric functions exhibits its superiority when compared to conventional designs. It offers a systematic and straightforward approach to construct a balanced and efficient design for studying the relationships between multiple variables. The design's rotatability ensures flexibility in experimental settings, making it a valuable tool for researchers and practitioners in various fields.
},
year = {2024}
}
TY - JOUR T1 - Construction of Twenty-Three Points Second Order Rotatable Design in Three Dimensions Using Trigonometric Functions AU - Dennis Mwan Matundura AU - Mathew Kosgei AU - Robert Too Y1 - 2024/05/24 PY - 2024 N1 - https://doi.org/10.11648/j.ajtas.20241303.11 DO - 10.11648/j.ajtas.20241303.11 T2 - American Journal of Theoretical and Applied Statistics JF - American Journal of Theoretical and Applied Statistics JO - American Journal of Theoretical and Applied Statistics SP - 46 EP - 56 PB - Science Publishing Group SN - 2326-9006 UR - https://doi.org/10.11648/j.ajtas.20241303.11 AB - In this paper, a novel twenty-three-point second-order rotatable design is formulated utilizing trigonometric functions. Design of experiments plays a crucial role in various industries and research fields to investigate the relationship between multiple variables and their effects on a response variable. In particular, second order rotatable designs are widely used due to their ability to efficiently estimate the main, interaction, and curvature effects. Nevertheless, creating designs with a substantial number of points poses difficulties. This study concentrates on developing a second-order rotatable design with twenty-three points utilizing trigonometric functions. Trigonometric functions offer a systematic approach to distribute the points uniformly in the design space, thereby ensuring the optimal coverage of the experimental region. The proposed construction utilizes the properties of sine and cosine functions to generate a balanced and efficient design. The methodology involves dividing the design space into equidistant sectors and assigning the points using the trigonometric functions. By carefully selecting the starting angle and the angular increment, a complete and orthogonal design is achieved. The design is rotatable, meaning it can be rotated to any desired orientation without impairing the statistical properties of the design. Through this construction, the design effectively captures the main effects, interaction effects, and curvature effects. This enables reliable estimation of the model parameters, leading to accurate predictions and efficient optimization. Additionally, the design is efficient in terms of minimizing the number of experimental runs required, thereby reducing costs and time. The suggested second-order rotatable design comprising twenty-three points and employing trigonometric functions exhibits its superiority when compared to conventional designs. It offers a systematic and straightforward approach to construct a balanced and efficient design for studying the relationships between multiple variables. The design's rotatability ensures flexibility in experimental settings, making it a valuable tool for researchers and practitioners in various fields. VL - 13 IS - 3 ER -